在建筑和工程的世界里,梁的挠度是一个至关重要的概念。它不仅关系到结构的安全,还影响着使用者的舒适度。想象一座桥梁如果过度挠曲,行人和车辆经过时都会感到不安全。同样,一栋大楼如果梁的挠度过大,居住者可能会感受到明显的震动。因此,理解和计算梁的挠度对于工程师来说是一项基本技能。今天,我们就来深入探讨一下20种常见梁的挠度计算,看看这些公式如何帮助我们确保结构的安全与稳定。
挠度的基本概念

在开始深入探讨各种梁的挠度计算之前,让我们先简单了解一下挠度的基本概念。挠度是指梁在受力后,其轴线在垂直于轴线方向的线位移。简单来说,就是梁弯曲的程度。挠度的大小受到多种因素的影响,包括梁的长度、截面的尺寸、材料的性质以及所受的荷载类型和大小。
常见梁的挠度计算公式
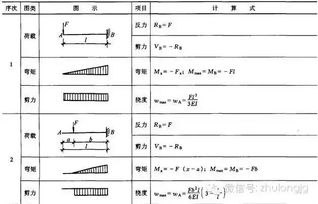
1. 简支梁在均布荷载作用下的挠度
对于简支梁,如果受到均布荷载的作用,其跨中的最大挠度可以通过以下公式计算:
\\[ Y_{max} = \\frac{5ql^4}{384EI} \\]
这里,\\( q \\) 是均布荷载的大小,\\( l \\) 是梁的长度,\\( E \\) 是材料的弹性模量,而 \\( I \\) 是梁的截面惯性矩。
2. 简支梁在集中荷载作用下的挠度
当简支梁受到集中荷载作用时,跨中的最大挠度计算公式为:
\\[ Y_{max} = \\frac{FL^3}{48EI} \\]
其中,\\( F \\) 是集中荷载的大小。
3. 悬臂梁在集中荷载作用下的挠度
悬臂梁是一端固定,另一端自由的梁。在自由端受到集中荷载作用时,其自由端的挠度可以通过以下公式计算:
\\[ Y_{max} = \\frac{FL^3}{3EI} \\]
4. 外伸梁在均布荷载作用下的挠度
外伸梁是一种具有外伸部分的梁。在均布荷载作用下,其挠度计算较为复杂,需要根据外伸部分和主梁的长度、荷载分布等因素来确定。
5. 连续梁的挠度
连续梁是指具有多个支座的梁。连续梁的挠度计算通常需要使用力矩分配法或弯矩系数法。这些方法可以考虑到连续梁的多个支座和荷载分布,从而更准确地计算出梁的挠度。
挠度计算的实际应用
了解了这些常见的梁挠度计算公式后,我们来看看它们在实际工程中的应用。例如,在桥梁设计中,工程师需要根据桥梁的长度、荷载以及材料的性质来计算梁的挠度,以确保桥梁在承受车辆和行人的重量时不会过度弯曲。
同样,在建筑设计中,梁的挠度计算也是必不可少的。工程师需要确保梁的挠度在安全范围内,以保护建筑物的结构和居住者的安全。此外,在机械设计中,梁的挠度计算也用于确保机械部件的稳定性和可靠性。
挠度计算的挑战
尽管梁的挠度计算公式看起来简单,但在实际工程中,工程师们仍然面临着许多挑战。首先,梁的挠度受到多种因素的影响,包括梁的长度、截面的尺寸、材料的性质以及所受的荷载类型和大小。这些因素的变化都会影响到挠度的计算结果。
其次,实际工程中的梁往往受到复杂的荷载作用,如风荷载、地震荷载等。这些荷载的作用方式复杂多变,需要工程师们使用更高级的计算方法来准确计算梁的挠度。
梁的挠度计算是工程中的一项重要任务,它关系到结构的安全和稳定。通过了解和掌握常见的梁挠度计算公式,工程师们可以更准确地计算出梁的挠度,从而确保结构的安全和稳定。虽然挠度计算在实际工程中面临着许多挑战,但通过不断学习和实践,工程师们可以不断提高自己的计算能力,为工程实践提供更好的服务。





